[Go up]
一般的にローンの支払方法には元利均等と元金均等（あるいは元本均等）がある。元利均等は毎月の支払額（元本＋利息）が一定（均等）になる方式。元金均等は毎月一定の元本と、それに利息を上乗せした額を支払う方式。元本の残高は支払いごとに減っていくため、それに一定の利率をかけた利息も支払いごとに減っていく。支払額から利息を引いたものを元本に充当するのが元利均等。元金均等は毎月の支払額が徐々に減っていく。
同じ利率・金額・期間のローンを組むと、最初のうちの支払額は元利均等の方が元金均等よりも少なくなる。しかし、元本の減り方が元金均等の方が早いため、利息も元金均等の方が早く少なくなる。従って、総支払額は元金均等の方が少なくなる。ただし、住宅ローン控除の税額控除の額は年末ローン残高の1%という計算のしかたをするため、元本の減り方の遅い元利均等の方が多くなる。
余談だが、変動金利で元利均等を選択している場合、利率が上がると利息を返しきれなくなって（いわゆる未払利息が発生して）借金が増えてしまう場合がある。元金均等の場合は元金が必ず減っていくから、借金が増えてしまうことはないはずである。
1. 元本充当分を求める。これは借入額を支払い回数で割ったもの。
2. 利息を求める。これはローン残高に毎回の利率をかけたもの。
3. 支払額を求める。1.と2.を足したものが支払額。
4. ローン残高は1.で求めた額だけ減る。
1. 利息を求める。これはローン残高に毎回の利率をかけたもの。
2. 元本充当分を求める。毎月支払い額から1.を引いたもの。
3. ローン残高は2.で求めた額だけ減る。
ここで問題になるのは、元利均等の毎月の支払額はどうやって決めてるの？ということである。元金均等の場合は借入金額と支払い回数が決まれば、毎月の支払額は簡単に計算できる。しかし、元利均等の場合はそうはいかないのである。まあ、返済額を早見表から求めればだいたいのローン返済シミュレーションはできるのだが、気になるところではある。
元本（借入金残高）をy、毎月の支払額をp、毎回の利率をr（単位は%ではなく倍率そのもの）、支払い回数をnとする。y[i]と書いた場合、i回支払いを終えた時の残高を示すことにする。y[0] は一回も支払ってないから借入金そのものである。一回目の利息は y[0]*r である。支払額はpだから、一回目の元本充当分は p-y[0]*r である。一回目支払い後の借入金残高は y[0] - (p-y[0]*r) になる。ちょっと書き換えると、
| y[1] | = y[0] - (p-y[0]*r) | ||
| = y[0] - p + y[0]*r | |||
| = y[0] + y[0]*r - p |
| （つまり、利息を足してから支払額を引いた形だ） | |
| = (1+r)*y[0] - p |
こうなる。y[1] は分かったので、y[2] を求める。やり方は同じ。y[1] に利息をかけ、支払額 p から利息を引いたものが元本充当分であり、これを y[1] から引いたものが y[2] になる。
| y[2] | = y[1] - (p-y[1]*r) |
| = y[1] - p + y[1]*r | |
| = y[1] + y[1]*r - p | |
| = (1+r)*y[1] - p |
右辺の y[1] にさっき求めた y[1] を入れてみる。
| y[2] | = (1+r)*y[1] - p |
| = (1+r) * { (1+r)*y[0] - p } - p | |
| = (1+r)*(1+r)*y[0] - (1+r)*p - p | |
| = (1+r)2 * y[0] - (1+r)*p - p |
これを次々に繰り返す。
| y[3] | = (1+r)*y[2] - p |
| = (1+r) * { (1+r)2 * y[0] - (1+r)*p - p } - p | |
| = (1+r)*(1+r)2*y[0] - (1+r){ (1+r)*p - p } - p | |
| = (1+r)3*y[0] - (1+r)*(1+r)*p - (1+r)*p - p | |
| = (1+r)3*y[0] - (1+r)2*p - (1+r)*p - p | |
| y[4] | = (1+r)*y[3] - p |
| = (1+r) * { (1+r)3*y[0] - (1+r)2*p - (1+r)*p - p } - p | |
| = (1+r)*(1+r)3*y[0] - (1+r)*(1+r)2*p - (1+r)*(1+r)*p - (1+r)*p - p | |
| = (1+r)4*y[0] - (1+r)3*p - (1+r)2*p - (1+r)*p - p |
原理的にはy[n]まで繰り返せばなんか方程式ができるはずだが、ひとつ進めるごとに項がひとつ増えちゃうので、これは現実的ではない。でも、よく見ると、後ろの ほげ*p の項は、初項 p、公比 (1+r) の等比級数が並んだ形だ。面倒なので初項1、公比Rの等比級数 n 項の和をS(R, n)で表しておくことにすると、
| y[4] | = (1+r)4*y[0] - (1+r)3*p - (1+r)2*p - (1+r)*p - p |
| = (1+r)4*y[0] - p * { (1+r)3 + (1+r)2 + (1+r) + 1 } | |
| = (1+r)4*y[0] - p * { 1 + (1+r) + (1+r)2 + (1+r)3 } | |
| = (1+r)4*y[0] - p * S(1+r, 4) |
とても簡単になる。これをy[n]まで繰り返す・・・のだが、繰り返すまでもなく、4 を n に置き換えてしまえばよい。
| y[n] | = (1+r)n*y[0] - p * S(1+r, n) |
さて、y[n] は何か？ というと、n 回支払いを終えた後の借入金残高である。n 回支払ってるわけだから、支払いはこれで終わっているはずである。つまり、借入金残高 y[n] は 0 でなければならない。従って、次のような方程式ができる。
(1+r)n*y[0] - p * S(1+r, n) = 0
これを p について解けばいいわけだ。
| (1+r)n*y[0] - p * S(1+r, n) | = 0 |
| - p * S(1+r, n) | = - (1+r)n*y[0] |
| p * S(1+r, n) | = (1+r)n*y[0] |
| p | = (1+r)n*y[0] / S(1+r, n) |
S(R, n)は等比級数の和だから、こうやって求める。
| S(R, n) | = 1 | + R | + R2 | + ... | + Rn-1 | ||
| - ) | R*S(R, n) | = | R | + R2 | + ... | + Rn-1 | + Rn |
|
|||||||
| S(R, n) - R*S(R, n) | = 1 | - Rn | |||||
| (1-R) * S(R, n) | = 1 - Rn | ||||||
| S(R, n) | = (1-Rn) / (1-R) | ||||||
求めたいのは S(1+r, n) だから、R に 1+r を入れて計算すると、
| S(1+r, n) | = { 1 - (1+r)n } / { 1 - (1+r) } |
| = { 1 - (1+r)n } / (-r) | |
| = { (1+r)n - 1 } / r |
これを元の式に入れて、
| p | = (1+r)n * y[0] / S(1+r, n) |
| = (1+r)n * y[0] / [ { (1+r)n - 1 } / r ] | |
| = (1+r)n * y[0] * r / { (1+r)n - 1 } |
| p = | (1+r)n * r | * y[0] |
|
||
| (1+r)n - 1 |
こうなる。例えば、借入額100万円、年利2.6%、30年払とすると、r = 2.6/100/12 = 0.0021667、n = 30*12 = 360 であるから、
| (毎月の支払額) | = (1+0.0021667)360 * 0.0021667 / { (1+0.0021667)360 - 1 } * 1000000 |
| = 4003. |
となる。公庫の早見表を見てみると確かに4003円になっている。
高校数学の漸化式のとてもよい課題である。こういう問題をもっとたくさん扱えば、数学も面白くなるんじゃないかなぁ。
公庫は10年たつと年利が4%に上がる。このときの支払い額はどうなるのだろうか？ 上の式の r に4.0/100/12を入れればよい？ 答えは×。なぜか。ひとつはローンを10年間一生懸命返してきたわけだから、借入金残高が減っている。返済期間も全体で30年という約束だったから、残りは20年になっている。したがって、年利2.6%でy[120]を計算してから、それを新たな元本として年利4%・n=240回でpを計算しなおさなければならない。
y[120]については、先ほどの漸化式から求めた結果が使える。
| y[i] | = (1+r)i * y[0] - p * S(1+r, i) |
| y[i] | = (1+r)i * y[0] - p * { (1+r)i - 1 } / r |
| (10年目の借入残高) | = y[120] |
| = (1+0.0021667)120 * 1000000 - 4003 * { (1+0.0021667)120 - 1 } / 0.0021667 | |
| = 748653. |
残高は748,653円。支払い期間は1/3過ぎたのに、借入残高は3/4くらい残っている。これが元利均等方式の特徴である。この先は r = 4.0/100/12 = 0.0033333、n = 20*12 = 240 なので、
| (10年目からの支払額) | = (1+0.0033333)240 * 0.0033333 / { (1+0.0033333)240 - 1 } * 748653 |
| = 4536. |
となる。これも公庫の早見表を見ると確かに4536円になっている。
ボーナス払いは年二回というだけである。たとえば、100万円を年利2.6%のボーナス払いだけで30年払にすると、各回の利率は r = 2.6/100/2 = 0.013、支払回数は n = 30*2 = 60 である。これをさっきの式に入れれば、
| (ボーナス払の支払額) | = (1+0.013)60 * 0.013 / { (1+0.013)60 - 1 } * 1000000 |
| = 24106. |
となる。これも公庫の早見表を見ればあっていることが分かるだろう。年あたりの支払額を比べると、毎月払が4003*12=48036円、ボーナス払いは24106*2=48212円で、毎月払の方が一年あたり176円だけ得なことも分かる。1000万円借りて10年間で17600円という些細な差ですが。
実際には初回支払までの利息の扱いなどで多少異なるはずなので、実際に借入する金融機関に確認のこと（借入月によってはボーナス払いの方が得の場合もある）。あんまり関係ないが、住宅ローン減税の事を考えると、ボーナス月は6月・12月で設定するより、1ヶ月遅らせて1月・7月で設定する方が有利のような気がする。案外、究極的には月払いなしで、12月借入、1月・7月のボーナス払いのみの方が得だったりして。
あんまり扱っているページを見たことがないので、以下は全部机上論。利息は返済間隔tに対してrの割合で単利で増えるとする。返済間隔tだけ時間が経つと、元金yにy*rの利息がつく。初回以外は常に返済間隔tで返済がなされるのでこれでよい。問題は借入から初回返済までの期間である。例えば、ボーナス払いで借入の次の日に初回返済がくるのと、ボーナスの直後に借り入れて半年後に初回返済が来るのとでは、半年分の利差がなければおかしい。
完全に初回から返済額を同じにしようとすると、ちょっと面倒な計算をしなければならない。しかし、実際には返済額を調整して対処しているようである。この場合、とりあえず何も考えずに初回の元本返済額を計算し、それに日割計算した利息を足して返済額を求めているようだ。
例えば、借入額100万円、年利2.6%、360回（30年）払、元利均等とした場合、毎回の返済額は4,003円 となり、初回利息は 1000000*2.6/100/12 = 2166.666円 だから、返済している元本は 4003 - 2166 = 1837円 となる。もし、借入日から初回返済日までが10日しかなかった場合、実際の利息は 1000000*2.6/100*10/365 = 712.328円 なので、これと元本返済額を足して 1837+712 = 2549円 が初回返済額となる。
ボーナス払いで、借入額100万円、年利2.6%、60回（30年）払、元利均等とした場合、毎回の返済額は24,106円となり、初回利息は1000000*2.6/100/2 = 13000円 だから、返済している元本は 24106 - 13000 = 11106円 となる。もし、借入日から初回返済日まで30日しか経っていない場合、実際の利息は 1000000*2.6/100*30/365 = 2136.986円 なので、これと元本返済額を足して 11106+2136 = 13242円 が初回返済額になる。
私の場合は、第1回支払日が通常の支払日と異なっており、第2回目も同様の計算がされていた。
|
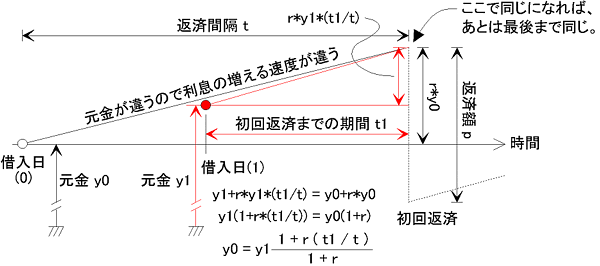
初回の返済額も二回目以降と同じにしたい場合は、例えば元利均等の場合を図にしてみるとこんな感じ。
借入額y0（黒）のパターンでは、借り入れてからちょうど返済間隔tだけ時間が経過して初回返済になった場合である。この図を見ると、今までの計算は全部このパターンだったことが分かる。一方、y1（赤）のパターンでは、借入からt1しか経っていないのに初回支払が来てしまっている。この場合、y0と同じように返済していたのでは利息を払いすぎてしまう。
本来の利息は、y0がy0*rだったのに対し、y1ではy1*r*(t1/t)のはずである。この利息の額と初回返済までの期間t1から、本来の元金y1を計算できる。そのためには、y0と利息y0*rの和と、y1と利息y1*r*(t1/t)の和が等しいという式を作ればよい。y0よりもy1の方が大きいから、初回返済まではy1の方が利息の増え方が速い。したがって、y0の利息増加直線の上にはy1の点はのらないことに注意。初回返済後はrとpが同じならば、あとは最後まで同じ経過をたどるはずである。
逆に、返済したい元金y1からy0の場合に変換すれば（図中の式）、あとは今までの説明で使ってきた式で返済額pが求まることになる。例えば、当初10年2.6%・元利均等ボーナス払いで100万円を借りたとする。先ほどの計算では24106円だった。これは、借入から6ヶ月後に初回返済が来る場合である。もし、借入の1ヶ月後に初回返済が来る場合は、
y0 = 1000000 * ( 1 + 0.013 * ( 1 / 6 ) ) / 1.013 = 989305.693
を、半年後初回返済で借りた場合と同じになる。元金相当額が安くなったのだから、返済額も安くなるはずである。試しに返済額を求め直してみると、
1.01360 * 0.013 / ( 1.01360 - 1 ) * 989305.693 = 23848.239
となって、毎回の返済額が258円ほど安くなることが分かる。
なお、元金均等の場合には、初回返済までの期間によらず、元金の返済額は初回も含めて毎回一定だから、違うのは初回利息だけのはずである。つまり、初回の支払額のみが計算と異なり、残りは全部計算通りになるはずだ。
計算結果が円単位ちょうどで端数が出ない、ということはほとんどなく、実際には小数以下に端数が出る。端数は切捨て・切上げ・四捨五入のいずれかで処理しなければならない。端数を処理すると当然誤差が出る。この誤差をどこかで調整しなければならない。
元金均等の場合、元金が支払い回数で割り切れてしまえば調整の必要はない。割り切れない場合は端数を初回・最終回のどちらかに回すか、あるいは毎回±1円の範囲で調整すればよい。
元利均等の場合、支払額は返済前に決められ、各回ごとに利息を計算して、支払額と利息の差額で返済元金が決まるため、総返済額（元金）に誤差が生じる。これを最後に調整しなければならない。例えば、借入額100万円、当初120回（10年）年利2.6%、以後4.0%、360回（30年）払、元利均等で、支払額と利息を切捨て計算してみる。
| 回 | 支払額 | 利息 | 返済額 | 残高 | 総支払額 |
|---|---|---|---|---|---|
| 1 | 4,003 | 2,166 | 1,837 | 998,163 | 4,003 |
| 2 | 4,003 | 2,162 | 1,841 | 996,322 | 8,006 |
「支払額」は「元利均等の計算」で説明した方法で計算しておく。前回の「残高」に毎回の利率（年利2.6%なので2.6/100/12 = 0.0021666...）をかけたものが「利息」となる。「支払額」から「利息」を引いたものが「返済額」となり、前回の「残高」から「返済額」を引いたものが今回の「残高」となる。また、前回の「総支払額」に今回の「支払額」を足したものが今回の「総支払額」となる。これを120回まで続けると、
| 回 | 支払額 | 利息 | 返済額 | 残高 | 総支払額 |
|---|---|---|---|---|---|
| 118 | 4,003 | 1,637 | 2,366 | 753,318 | 472,354 |
| 119 | 4,003 | 1,632 | 2,371 | 750,947 | 476,357 |
| 120 | 4,003 | 1,627 | 2,376 | 748,571 | 480,360 |
こうなるので、借入額748,571円、年利4.0%、240回払、元利均等で支払額を計算しなおす（4,536円になる）。続けて359回まで計算するとこうなる。
| 回 | 支払額 | 利息 | 返済額 | 残高 | 総支払額 | |
|---|---|---|---|---|---|---|
| 121 | 4,536 | 2,495 | 2,041 | 746,530 | 484,896 | |
| 122 | 4,536 | 2,488 | 2,048 | 744,482 | 489,432 | |
| 中略 | ||||||
| 358 | 4,536 | 44 | 4,492 | 8,914 | 1,559,928 | |
| 359 | 4,536 | 29 | 4,507 | 4,407 | 1,564,464 | |
最後の支払を目前にして残高は4,407円である。利息は4407*4.0/100/12 = 14.69円、したがって、最終回は 4407+14 = 4421円 を支払えばよく、毎回の支払額4536円とは誤差が生じることが分かる。
| 回 | 支払額 | 利息 | 返済額 | 残高 | 総支払額 |
|---|---|---|---|---|---|
| 360 | 4,421 | 14 | 4,407 | 0 | 1,568,885 |
ボーナス払いでも同様に計算できて、
| 回 | 支払額 | 利息 | 返済額 | 残高 | 総支払額 | |
|---|---|---|---|---|---|---|
| 1 | 24,106 | 13,000 | 11,106 | 988,894 | 24,106 | |
| 2 | 24,106 | 12,855 | 11,251 | 977,643 | 48,212 | |
| 中略 | ||||||
| 18 | 24,106 | 10,272 | 13,834 | 776,386 | 433,908 | |
| 19 | 24,106 | 10,093 | 14,013 | 762,373 | 458,014 | |
| 20 | 24,106 | 9,910 | 14,196 | 748,177 | 482,120 | |
| 21 | 27,350 | 14,963 | 12,387 | 735,790 | 509,470 | |
| 22 | 27,350 | 14,715 | 12,635 | 723,155 | 536,820 | |
| 中略 | ||||||
| 58 | 27,350 | 1,577 | 25,773 | 53,081 | 1,521,420 | |
| 59 | 27,350 | 1,061 | 26,289 | 26,792 | 1,548,770 | |
最終回は利息 26792*4.0/100/2 = 535.84円 と残高26,792円を足して、支払額は27,327円となる。
| 回 | 支払額 | 利息 | 返済額 | 残高 | 総支払額 |
|---|---|---|---|---|---|
| 60 | 27,327 | 535 | 26,792 | 0 | 1,576,097 |
以下は余談。月払いとボーナス払いの総支払額を比べてみると、1568885-1576097=-7212 となるから、月払いの方が7,212円総支払額が少ない。一般的に「月払いとボーナス払いでは月払いの方が得」とされている論拠はここにある。
しかし、もし借りた直後に初回返済が来れば、初回利息はほぼゼロになる。初回利息を見ると月払いが2,166円、ボーナス払いが13,000円となっているから、その分を引くと、月払いは 1568885-2166 = 1566719円、ボーナス払いは 1576097-13000 = 1563097円 が総支払額となる。比べると、1566719-1563097 = 3622 となり、ボーナス払いの方が3,622円総支払額が少ない。
つまり、時と場合によって、月払い・ボーナス払い、どちらが得か？ は変わることになる。税額控除も考えると、12月に融資が実行され、1月の最初の方に初回支払が来るボーナス払いのパターンが一番お得になると考えられる。実際には融資実行時期は自由にならないため、運を天に任せるしかないのだが。
Copyright (C) 2002-2007 You SUZUKI
$Id: loan.htm,v 1.3 2008/07/06 09:50:44 you Exp $