大学の一年次で交流回路理論を習った。 そのときに出くわしたのがこれ。
ここで \(j\) は虚数単位。 数学で \(i\) と書くアレ。 電気電子系では \(i\) と書くと電流と紛らわしいので \(j\) と書く習慣になっている。 \(e^{j \omega t}\) はオイラーの公式で \(\cos \omega t + j \sin \omega t\) になる。 これは大学に入って複素解析学をやると一番最初に出てくる。 高校ではやらないが、形式的な導出は高校の微積分まで習っていればできる(そして知っているといろいろと便利)。 ここまではいい。 問題は、現実世界の事象を扱うのに、なんで電圧を複素数で表現するの? ということ。 大学在学中には納得のいく考えは浮かばなかった。 便利だから使ってたけど。
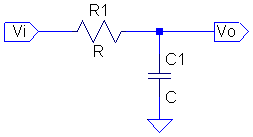
例えば、こんな簡単な回路。

この回路の出力電圧は、R1のインピーダンスが \(R\) 、C1 の(複素)インピーダンスが \(1/j \omega C\) だから、直流回路と同じように分圧回路の計算式を使って、
と計算する。 でも、 \(V_i\) は \(\cos \omega t\) とかなわけで。 それに複素数を乗じたら \(V_o\) は複素数になってしまうではないか・・・。 \(V_i = e^{j \omega t}\) とおいて、結果の実部だけとればよいと言われても、虚部の立場はいったい・・・。
さっきの回路の \(V_o\) を実数の中で解いたらどうなるだろう? 今は出力には電流を流していないという仮定で計算してるから、入力からR1を流れた電流は、そのままC1を通ってグランドに流れる。 そして、電流路はこれだけなので、これを \(i\) とする。 \(i\) は抵抗の両端の電位差 \(V_i - V_o\) と抵抗値 \(R\) から簡単に求まる。 \(i\) を積分するとコンデンサ両端の電圧になるが、コンデンサの片方の端子はグランドで、もう一方は出力につながってるので、これは出力電圧になる。
両辺を微分すると、
となるので、これを根性で解く。 1階微分方程式なので、解くと任意定数がひとつ出てくる。 これは初期状態でコンデンサに溜まっている電荷に相当し、時間とともに指数関数的に減衰する挙動を示すはずだが、今は交流回路を解析してるので直流のことは忘れる。 つまり、コンデンサの電荷、そして出力電圧の平均値は0でいいことにする。
入力を振幅 \(A\) 、角周波数 \(\omega\) の正弦波(余弦波) \(v_i = A \cos \omega t\) とすると、この回路の中に周波数を二倍にしてしまったり、半分にしてしまったりする素子はないので、出力も角周波数 \(\omega\) の正弦波になるはず。 ただ、振幅と位相は変化するので、きっと \(v_o = B \cos (\omega t + \theta)\) という形になる。 ここで、 \(A, B\) は振幅なので負ではない実数。 これを微分方程式に代入して、 \(C\) ・ \(R\) ・ \(A\) ・ \(\omega\) から \(B\) と \(\theta\) を表す式を求めればいいだろう、きっと。 代入してみると、
・・・ \(\sin\) と \(\cos\) がごちゃ混ぜになってしまった。 どうしよう。 とりあえず加法定理でバラすしかなさそうだが、このままだとふたつバラすハメになるので、 \(\omega t + \theta = \omega \tau\) と変数を変換して、バラす量を減すことにする。 \(\omega t\) は \(\omega \tau - \theta\) になるから、
これを \(\cos \omega \tau\) と \(\sin \omega \tau\) に注目してまとめる。 \(CR\) もいいかげん左辺に移しておくか。
これが \(\tau\) によらず成り立たないといけないから、 \(\sin \omega \tau\) の係数と \(\cos \omega \tau\) の係数が両辺で等しくないといけない。 したがって、
より、
つまり、
さらに、 \(\cos^2 \theta + \sin^2 \theta = 1\) より、
これで \(\theta\) と \(B\) が求まった(よかった)。 つまり、振幅は \(1 / \sqrt{ ( CR \omega )^2 + 1 }\) 倍になり、位相は \(\tan^{-1}\omega CR\) だけ遅れる、ということが分かる。
入力が \(A \cos (\omega t + \alpha)\) の形だった場合、 \(\omega t + \alpha\) を新たに \(\omega \tau\) とでも置けば、出力は \(B \cos (\omega \tau + \theta)\) で、 \(\theta = -CR \omega\) になり、 \(\omega \tau\) を元に戻せば、 \(B \cos (\omega t + \alpha + \theta)\) になることが分かる。 これで任意の振幅・位相の正弦波について出力を求めることができた。
・・・じゃぁ、正弦波じゃなかった場合は?
ここで少し「線形」について考えてみる。 「線形」というのは、一般的には以下の性質のことを言いうらしい。
関数 \(f(x)\) が以下の性質を満たすとき、この関数は「線形である」という。
任意の数 \(a, b\) について、 \(f(a+b) = f (a) + f (b)\)
任意の数 \(c, x\) について、 \(f (cx) = c \cdot f (x)\)
「線形」と言われて訳が分からなくなったら、とりあえずこの定義に戻って考えればなんとかなる。
で、「線形な回路」とはなんだろう? ある回路に \(v_{i1}(t)\) を入力したときに出力 \(v_{o1}(t)\) が得られ、 \(v_{i2}(t)\) を入力したときに出力 \(v_{o2}(t)\) が得られたとする。 \(k\) を任意の定数して、この回路が「線形である」ならば、
入力として \(v_{i1}(t) + v_{i2}(t)\) を加えると、出力 \(v_{o1}(t) + v_{o2}(t)\) が得られる。
入力として \(k \cdot v_{i1}(t)\) を加えると、出力 \(k \cdot v_{o1}(t)\) が得られる。
が成り立つ。 当たり前のようだが、例えば回路網にダイオードやトランジスタが入ったら、もうこの回路は線形ではなくなる。 線形であることは当たり前ではない。
では、この回路は線形なのだろうか? この回路では、微分方程式
が成り立っているので、適当な入力 \(v_{i1}(t)\) と \(v_{i2}(t)\) を用意して、その出力を \(v_{o1}(t)\) と \(v_{o2}(t)\) とすると、以下の関係が成り立っている。
第1式の両辺を \(k\) 倍すれば、
となって、元の方程式と比べると、入力に \(k \cdot v_{i1}\) を加えると出力が \(k \cdot v_{o1}\) になることが分かる。 一方、2つの方程式を左辺・右辺をそれぞれ足すと、
となるので、これも元の方程式と比べると、入力に \(v_{i1} + v_{i2}\) を加えると出力が \(v_{o1} + v_{o2}\) になることが分かる。 微分も線形演算だからこうなる。 結局、この回路は線形で、入力が複数の信号を加算した形になっていた場合、それぞれの入力信号に対する出力を求め、その和をとれば全体の出力が求まる。
そして、たいていの周期波形はフーリエ級数に展開でき、適当な振幅と位相の正弦波に分けることができる。 フーリエ級数の書き方にはいくつかのパターンがあるが、角周波数 \(\omega\) の周期波形 \(v_i(t)\) は、フーリエ級数に展開すると、例えば以下のように書ける。
まぁ、 \(\sin\) と \(\cos\) の和で書くのが普通だけど。 気に入らなければそれぞれの項を加法定理で展開すればいい。 \(n = 0\) のときは \(\theta_0\) は0として、そうすると \(\cos\) は常に1になるので、 \(A_0\) は直流成分。 この信号を線形な回路に入力した場合、その出力はおのおのの正弦波に対する出力の和になる。 それぞれの出力の振幅を \(B_n\) 、位相差を \(\theta_n\) とすれば、出力 \(v_o(t)\) は、
で求まる。 これでどんな周期波形でも(フーリエ級数にできれば)解決。
これを複素数で考え直す。 入力 \(v_i\) は複素指数関数 \(A e^{j\omega t}\) になる。 出力 \(v_o\) はきっと \(B e^{j (\omega t+\theta) }\) になるに違いない。 微分方程式は実数のときと同じだから、早速代入してみる。
指数関数は微分しても指数関数というところがミソなんだな。
冒頭の式の形になった。 実数のときと比べてめっちゃ簡単。 これが複素数を使う場合のメリットらしい。
このままだと振幅と位相が分かりにくいので分母を実数化して、
振幅の2乗 \(|v_o/v_i|^2\) は、 \(|a+bj|^2 = a^2+b^2\) より、
位相は \(\tan \theta\) は虚部/実部なので、 \((\ref{eqn1})\) の分子から、
振幅と位相、どちらも確かに実数のときと同じになる。 でも複素指数関数と \(\cos \omega t\) 、結局どういう関係?
この回路は複素数の世界でも線形だ。 線形かどうか確かめるときに「入力・出力が実数とすると」とは一言も言ってないから。 現実の回路が複素数でどうなるかを考えるのもなんか変だけど。 あとは複素数の世界でもフーリエ級数展開があれば、どんな周期波形でも出力が求められる。
複素数でのフーリエ級数は以下のようになってるらしい。
実数の場合と比べて \(\cos\) が複素指数関数になるのは当然として、他にもいくつか違いがある。 まず、 \(n\) の範囲が \(-\infty \) からになっている。 実数の世界では 例えば \(\sin(-x) = -\sin(x)\) なので、 \(n\) は負にする必要がなく、 \(A_n\) の範囲に負の実数を含めれば十分。 一方、複素指数関数の場合、 \(e^{-j \omega t}\) に \(\omega\) と関係のない定数をかけて \(e^{j \omega t}\) にすることがどうやってもできないので、 \(n\) が負の場合も考える必要があるらしい。 ちなみに、 \(e^{j \omega t}\) と \(e^{-j \omega t}\) は複素共役の関係にある。
それと、 \(\alpha\) がなくなってしまった。 \(e^{j(n \omega t+\alpha_n)}\) と書きたいところだが、これは \(e^{j\alpha_n} \cdot e^{jn \omega t}\) のことなので、 \(e^{j\alpha_n}\) の部分を \(C_n\) に含めることができる。 つまり、 \(C_n\) は複素数で、角周波数 \(\omega_n\) の複素指数関数の振幅と位相を同時に表している、と考えられる。
もうひとつ、実数のフーリエ級数では複素数の関数は表現できない(当然)が、複素数のフーリエ級数では実数も表現することができる。 例えば、 \(\cos \omega t\) は \((1/2) (e^{j \omega t} + e^{-j \omega t} )\) になる。 これが正しいことはオイラーの公式を使えばすぐに分かる。 フーリエ級数だと思えば、 \(C_{1}\) と \(C_{(-1)}\) が \(1/2\) ということになる。 この例でも \(n\) に負の範囲が必要だということが分かる。
オイラーの公式から、
で、今は線形な回路を考えているので、 \(v_i = A \cos (\omega t)\) に対する出力を求めたければ、 \(v_i = e^{j \omega t}\) と \(v_i = e^{-j \omega t}\) に対する出力を計算して、足して、 \(A\) をかけて2で割ればいいことになる。
\(v_i = e^{j \omega t}\) の場合は、先ほどの計算結果 \((\ref{eqn1})\) から
になる。 一方、入力が \(v_i = e^{-j \omega t}\) の場合、 \(\omega\) は正であるなんて約束した覚えはないから、計算しなおす必要はなくて、 \(\omega\) に \(- \omega\) を突っ込んでしまえばよい。
\(v_o(\omega)\) と \(v_o(-\omega)\) を見比べると、分数の部分が複素共役になっていて、 \(e^{j\omega t}\) と \(e^{-j\omega t}\) は複素指数関数の性質からやはり複素共役なので、 \(v_o(\omega)\) と \(v_o(-\omega)\) は複素共役になることが分かる(よく分からない人は \((a+bi)(c+di)\) と \((a-bi)(c-di)\) が複素共役になることを自分で確かめること)。 ということは、 \(v_o(\omega)\) と \(v_o(-\omega)\) を足すとちゃんと実数になる。
入力が \(v_i = A \cos(\omega t + \theta)\) だった場合は、オイラーの公式から、
になって、 \(e^{j\theta}\) と \(e^{-j\theta}\) は定数なので、 先ほどの結果と線形な回路の性質から、 この式の \(e^{j\omega t}\) と \(e^{-j\omega t}\) の部分を、先ほどの \(v_o(\omega)\) と \(v_o(-\omega)\) の結果に置き換えてやれば速攻で出力が求まり、
になることが分かる。 分数の部分も、ふたつの複素指数関数も複素共役だから、やはりカッコの中のふたつの項は複素共役になることが分かる。 したがって \(v_o\) はやはり実数になり、 \(A/2\) はもちろん実数だから、全体もちゃんと実数になる。
結果がたまたま実数に戻っただけじゃないの? という疑問が残るが、数学的に考えて、
は常に成り立つ式である。 右辺は複素指数関数で書いてあるが、左辺と等しいのだから、計算すれば虚部は消えて必ずなくなる。 出力はここから微分方程式から求めたが、微分方程式に虚数が出てくる要素はどこにもないから、 \(v_i\) が実数なら \(v_o\) も実数のはず。 計算途中で複素指数関数があったとしても、線形である限り、計算を間違えない限り、結果は必ず実数になる。 なので、結果が実数になったのは偶然ではなくて必然である。
どうして複素共役になったかを考えると、 \(\omega\) が必ず虚数単位 \(j\) を伴っているからだ。 これは \(e^{j\omega t}\) を微分したときに出てきた係数で、2階微分すると実数に、3階微分するとまた虚数になる。 つまり、偶数階微分で実数、奇数階微分で虚数になるが、 \(\omega\) は偶数階微分の時には偶数乗になるから、 \(\omega\) が正でも負でも結果は正になる。 奇数階微分の時には \(\omega\) は奇数乗になり、 \(\omega\) が正ならば正、負ならば負になる。 したがって、実部は正、虚部は \(\omega\) の符号に従うことになって、 \(\omega\) の正負について計算すると必ず複素共役になる。
一方、実関数を複素フーリエ級数に展開すると、結果は \(\omega\) が正負の位置に必ず複素共役で現れることになっている。 \(\cos\omega t\) は \((1/2)e^{j\omega t}+(1/2)e^{-j\omega t}\) だから \(+\omega\) と \(-\omega\) の係数は実数で符号が同じになり、 \(\sin\) については \(e^{j\omega t}-e^{-j\omega t}=2j\sin\omega t\) だから、
となり、 \(+\omega\) と \(-\omega\) の係数は純虚数で、 \(+\omega\) だけ符号が逆になる。 実数のフーリエ級数はこの式を使えば簡単に複素フーリエ級数の形に直すことができ、このとき \(+\omega\) の虚部だけ符号が逆になるので、必ず複素共役になる。
このため、入力が実数なら、複素指数関数で \(+\omega\) と \(-\omega\) に対して計算していくと、両者の結果は必ず複素共役になり、和をとると虚部が消えてなくなる。 結果が複素共役になると分かっているのなら、 \(-\omega\) に関する計算はムダで、 \(+\omega\)に対してだけ計算すればよくて、しかも虚部はなくなると分かっているので、その実部をとれば十分。
結局、入力が \(e^{j\omega t}\) のときに、出力が \(Ke^{j\omega t}\) になる(ただし \(K\) は複素数で、通常は \(\omega\) の関数)ことが分かれば十分で、振幅は \(K\) の絶対値倍に、位相は \(K\) の偏角だけ進む(マイナスなら遅れる)ことになる。 世の中ではこれをフェーザ表示と言うらしい。 大学時代はこれが当たり前だったから、「フェーザ表示で表すと・・・」のような文句はほとんど使わなかったけど。 この回路の場合は、
まで分かれば十分、ということになる。
普通、瞬時値( \(t\) の関数)の場合は電流・電圧は小文字で、実効値(二乗平均値)の場合は大文字で書くことになっている。 振幅だけでなく位相も実効値に含めることにして、それを複素数で表せば、これは実効値なのだから上のように大文字で表記することになる。
冒頭に挙げた式と、微分方程式を複素指数関数を使って解いた式、形が同じになった。 冒頭で挙げた式は微分方程式を使ってない。 なぜだろう?
各部品の電圧と電流の関係を複素指数関数で考えなおしてみると、抵抗は \(v=Ri\) で、これは \(v\) や \(i\) が複素数でもこのまま。 コンデンサは、電流を積分したものが電圧になるので、
これに \(v=e^{j\omega t}\) を代入して両辺を微分して計算を進めると、
\(e^{j\omega t}\) を \(v\) に戻してやると、
になる。 電圧と電流の関係がこうなっているから、信号源が \(e^{j\omega t}\) ならばこれをそのまま回路方程式に使って構わない、ということになりそうだ。 そうすれば、たとえば冒頭の回路では、入力からR1 - C1 - グランドと流れる電流を \(i\) とすると、微分や積分を使わずに出力電圧を \(v_o=i/j\omega C\) と書けて非常に楽だ。 R1については \(i=(v_i-v_o)/R\) という式が成り立つから、これを \(v_o\) の式に代入し、 \(v_o\) について解くと冒頭の式になる。
式を組み上げてから微分方程式を解くのではなく、個々の部品についてあらかじめ微分方程式を解いてから式を組み上げるような感じだろうか。 あらかじめ解くといっても、コンデンサとコイルについて1回だけ解けば、あとは定数が違うだけなので、一生に一度だけ解けば十分。 現象としてはどちらも同じものを記述してるから、結果は同じになるはず。
抵抗の場合の \(v=iR\) の式と、コンデンサの場合の \(v=i/j\omega C\) の式を比べると、コンデンサは抵抗値が \(1/j\omega C\) の抵抗のように振舞うことが分かる。 そこで、抵抗値に複素数を許し、コンデンサも抵抗も \(v=iR\) という式で電圧と電流の関係を表現できるようにしたものを、世の中では複素インピーダンスと呼ぶらしい。
抵抗値 \(R\) の抵抗のインピーダンスは
で、これは実数。
容量 \(C\) のコンデンサのインピーダンスは
になる。
コイルの場合は、
なので、電流を \(i=e^{j\omega t}\) とすると、先ほどと同様に計算して、
となるから、インダクタンスLのコイルのインピーダンスは
になる。
これらの複素インピーダンスを使えば、交流回路解析の上ではコンデンサもコイルも、抵抗と同じように扱える。 これで微分方程式を解く必要もなくなった。 そして、計算式から \(t\) が消える。 つまり、時間の関数であることも忘れてよさそうだ。 電圧・電流は実効値だけ考えていればよく、複素数になった場合は絶対値が振幅、偏角が位相を示す。 今までは電圧と電流をほとんど小文字で書いてきたが、これは瞬時値(時間の関数)として扱っていたから。 実効値として扱うなら、電圧と電流は大文字で書いて計算することになる。 複素数を使うことで計算が大幅に簡単になった。 やっぱり便利。
Copyright (C) 2011-2019 You SUZUKI
$Id: phasor.htm,v 1.10 2019/02/21 16:03:35 you Exp $